Fibonacci

Have you ever heard of the Fibonacci sequence? Or the golden ratio? Or the golden spiral?

These mysterious numbers and shapes are all connected to each other. If you look closely, they can be found in the most unexpected places, creating beautiful and appealing patterns.

Simply put, the Fibonacci sequence is a series of numbers starting with 1 and 1. From there, add the two previous numbers in the sequence to get the next number. This is a type of recursive sequence.

So 1+1=2, 1+2=3, 2+3=5 and so on. This gives you a sequence that looks like 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 etc. But what makes this sequence so special and interesting?

The mathematical sequence that governs nature

For starters, Fibonacci numbers can be found in the natural world around us. For example, most flowers will have a number of petals corresponding to the Fibonacci sequence. Irises have three petals while wild roses and buttercups have five petals. That is, of course, until a petal falls off. No wonder rare four-leaf clovers are considered lucky!

If you cut into a piece of fruit, you are likely to find a Fibonacci number there too, in how the sections of the seeds are arranged. Bananas have three parts while apples have five.

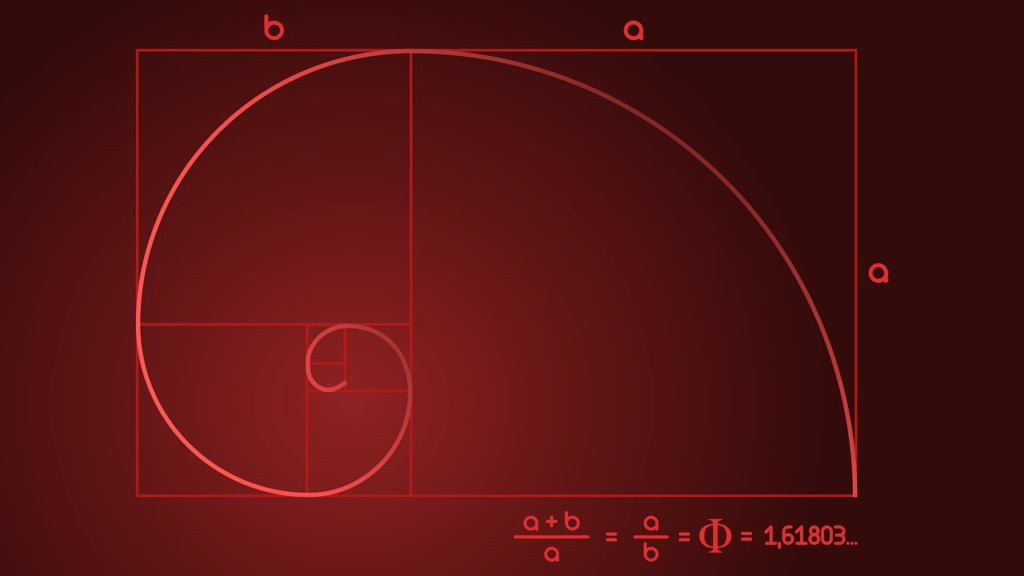
The Fibonacci sequence even plays a role in the subtle spirals you can see in the seed head of a sunflower. This is due to something called the golden ratio, the golden ratio or the Greek letter Phi. If you take a number in the sequence above 5, and divide it by the previous number, you get an answer very close to 1.618. The bigger the numbers, the closer you get to 1.618. The golden ratio is an irrational number, and therefore cannot be written as a fractional number. Again, this is a number that can be found in the natural world.

Take the sunflower. To be as effective as possible, its seeds must be packed tightly together without overlapping. Now, if it only grew seeds in a straight line in one direction, it would leave lots of empty space on the flower head. The best way to minimize waste of space is for the seeds to grow in spirals, with each seed growing at a slight angle away from the previous one.

If the degree of turn was a fraction, like 1/4, then it doesn’t matter because after four laps the seed pattern would be back at the beginning again. There would be four rows of seeds, but it’s not much better than one when trying to cover a circular area. The perfect degree of luck must be an irrational number, not easily approximated by a fraction, and the answer is the golden ratio.

The Fibonacci spiral can be found in art, architecture, biology and many more places

Turning numbers into an eye-catching spiral

Another way to think of the golden ratio is as a spiral. This spiral gets wider by a factor of 1.618 each time it makes a quarter turn (90°).

Drawing a perfect golden spiral is quite tricky to do by hand, but just like with the golden ratio, you can get a close approximation with the Fibonacci spiral. This is created by drawing an arc through a series of squares corresponding to the Fibonacci numbers, so 1², 1², 2², 3² etc.

You may have seen these spirals superimposed over famous works of art, as experts try to explain why we find them so aesthetically pleasing. Often the spiral pulls our eye so that the focus of the artwork is in the center of the spiral. Examples include works by Leonardo da Vinci and Salvador Dali.

Listen for the Fibonacci sequence in music

Fibonacci did not actually discover the sequence himself. Born Leonardo Bonacci in 12th century Pisa, Italy, the mathematician traveled extensively around North Africa. There he learned how the Hindu-Arabic numbers 0-9 could be used to make calculations easier than the Roman numerals still used in much of Europe. Fibonacci explained his discoveries in a book called Liber Abaci, published in 1202, which had a section dedicated to the intriguing sequence that would be named after him hundreds of years later.

However, Indian poets and musicians had already been aware of the Fibonacci sequence for centuries, having discovered its implications for rhythm and various combinations of long and short beats.

Mozart used the golden section when writing a number of his piano sonatas. A sonata can be divided into two separate sections, known as the exposition (where the theme is introduced) and the development and recapitulation (where the theme is developed and repeated). In Mozart’s sonatas, the number of bars in the latter part divided by the former is about 1.618, the golden mean.

There is even a style of poetry inspired by the Fibonacci sequence, known as Fib Poetry. Each line of the poem must contain the exact number of syllables corresponding to the Fibonacci sequence. So a six-line poem would have syllable lines of 1, 1, 2, 3, 5 and 8.

About the Viking

With Viking’s signals, you have a good chance of finding the winners and selling in time. There are many securities. With Viking’s autopilots, price data, tables and stock prices, you can sort out the most interesting ETFs, shares, options, warrants, funds, etc.

Click here to see what Vikingen offers: Detailed comparison – Stock market program for those who want to become even richer (vikingen.se)